10. Aufgabensammlung
In diesem Kapitel findest du eine Sammlung von Aufgaben. Die Aufgaben sind in vier Teilgebiete gegliedert.
Zu Beginn jeder Aufgabe sind die Vorkenntnisse angegeben,
d.h. welche Kapitel mal zum Lösen gelesen haben sollte.
Zu jeder Aufgabe gibt es eine Musterlösung.
Die Musterlösungen sind die *.py-files
und können heruntergeladen werden.
Die Kommentare am Anfang der Dateien können ignoriert werden.
Weiter gibt es jeweils noch eine Zusatzaufgabe, für welche keine Musterlösung vorhanden ist.
10.1. Allgemein
10.1.1. Hello World! I’m…
Vorkenntnisse: Kapitel 1.
Erstelle ein Programm, das deinen Vorname, Nachname und dein Geburtsdatum auf der Konsole ausgibt.
Musterlösung:
hello_i_am.py.
Zusatzaufgabe: Erweitere dein Programm, indem es zum Beispiel auch deine Adresse oder deine Telefonnummer ausgibt.
10.1.2. Winkelmass Umwandler
Vorkenntnisse: Kapitel 1 bis 3.
Schreibe ein Programm, das zu einem gegebenen Winkel im Bogenmass (Eingabe in der Konsole durch den Benutzer), den entsprechenden Winkel im Gradmass berechnet. Die Ausgabe soll mit Grad (°), Bogenminuten (') und Bogensekunden (") ausgegeben werden.
Hinweise:
Die Zahl \(\pi\) kann vom Modul
mathmit dem folgenden Befehl geladen werden:from math import pi. Der Wert ist dann in der Variablepigespeichert.Überlege dir, wie man die zwei Befehle
input()undfloat()benutzen kann, um eine Flieskommazahl einzulesen.
Musterlösung:
bogen_nach_gradmass.py.
Zusatzaufgabe: Schreibe ein Programm, welches die Umrechnung vom Gradmass ins Bogenmass übernimmt.
10.1.3. Temperatur Umwandler
Vorkenntnisse: Kapitel 1 bis 5.
Schreibe ein Programm, das Temperaturen in verschiedene Skalensystemen ineinander umwandelt. Das Programm soll zu Beginn eine Auswahl mit den verschiedenen Möglichkeiten anbieten:
(1) Umrechnung von Celsius nach Kelvin
(2) Umrechnung von Celsius nach Fahrenheit
(3) Umrechnung von Kelvin nach Celsius
(4) Umrechnung von Kelvin nach Fahrenheit
(5) Umrechnung von Fahrenheit nach Celsius
(6) Umrechnung von Fahrenheit nach Kelvin
Bemerkung
Dies kann dir sicher helfen.
Celsius = 5/9 * (Fahrenheit - 32).
Celsius = Kelvin - 273.15.
Die tiefste mögliche Temperatur ist den absoluten Nullpunkt
0K.
Hinweise:
Musterlösung: temperatur_umwandler.py.
Zusatzaufgabe: Passe deine Lösung aus der Aufgabe Winkelmass Umwandler so an, dass beide Umrechnungen (Bogen- nach Gradmass und umgekehrt) in einem einzelnen Programm möglich sind.
10.1.4. Mit Funktionen
Vorkenntnisse: Kapitel 1 bis 6.
Erweitere deine Lösung der vorherigen Aufgabe, indem du für die Umrechnung 6 verschiedene Funktionen definierst. Passe ausserdem dein Programm so an, dass der Benutzer mehrere Temperaturen nacheinander umrechnen kann und den Zeitpunkt zum Beenden des Programms selber bestimmt.
Hinweise:
Bei der Implementierung braucht man einige konstante Werte (zum Beispiel brauchst du in dieser Aufgabe den Wert des absoluten Nullpunktes -273.15 in Grad Celsius). Es lohnt sich solche Konstanten am Anfang des Programms zu definieren. In einigen Programmiersprachen gibt es sogar die Möglichkeit, "Variablen" zu definieren, deren Werte nicht geändert werden können. In Python gibt es diese Möglichkeit jedoch nicht. Per Konvention benennt der Entwickler die Konstanten mit grossgeschriebenen Buchstaben (z.B.
ABSOLUTER_NP_C = -273.15).Um nach einer gültigen Eingabe des Benutzers zu fragen, kannst du die folgende Funktion benutzen:
1def get_float(msg = "Bitte Zahl eingeben: "): 2 while True: 3 try: 4 f = float(input(msg)) 5 return f 6 except ValueError: 7 print("Ops! Ungültige Eingabe. Bitte nochmals probieren: ")
Diese Funktion hat ein optionales Argument
msg. Wenn die Funktion ohne Argumente aufgerufen wird, nimmtmsgden vorgegebenen Wert"Bitte Zahl eingeben: "an. Falls der Benutzer eine Zahl eingibt, so wird diese zurückgegeben. Andere Eingaben werden nicht akzeptiert: das Programm erkennt ungültige Eingaben mit der Ausnahmebehandlung (try-except) und fragt solange, bis eine gültige Eingabe getätigt wurde.Analog kannst du ungültige Eingabewerte für die Temperatur mit
raiseüberprüfen. Siehe folgendes Beispiel:1def Celsius_Kelvin(t): 2 if t >= ABSOLUTER_NP_C: 3 return t - ABSOLUTER_NP_C 4 else: 5 raise TypeError(FEHLERMELDUNG_TEMP)
Musterlösung: temperatur_umwandler_erweiterung.py.
Zusatzaufgabe: Erweitere die Lösung der vorherigen Zusatzaufgabe (Winkelmass Umwandler), indem du Funktionen implementierst.
10.1.5. Mit GUI
Vorkenntnisse: Kapitel 1 bis 8.
Versuche deine Lösungen von den vorherigen Aufgaben mit einer graphische Benutzeroberfläche zu erweitern. Das Fenster soll folgende Elemente enthalten:
ein OptionMenu Widget für die Wahl der Umrechnung (Celsius nach Kelvin, …).
ein Entry Widget, für die Eingabe der Temperatur.
ein Label Widget, für die Ausgabe.
ein Button Widget, der die Umrechnung startet.
Für die Erstellung des OptionMenus kannst du folgendes Muster anpassen:
1from tkinter import * 2 3fenster = Tk() 4 5variable = StringVar(fenster) 6variable.set("one") # default value 7 8w = OptionMenu(fenster, variable, "one", "two", "three") 9w.pack() 10 11fenster.mainloop()
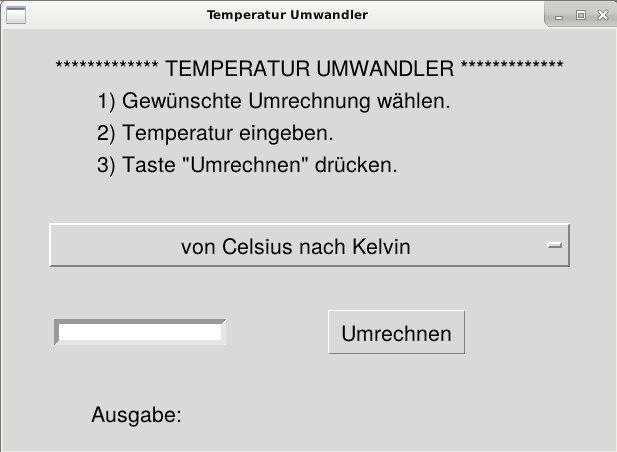
Beispiel eines möglichen Layouts des Fensters.
Musterlösung: temperatur_gui.py.
Zusatzaufgabe: Erstelle auch für den Winkelmass Umwandler ein GUI.
10.1.6. Sortierprogramm
Vorkenntnisse: Kapitel 1 bis 4.
Schreibe ein Programm, welches eine Liste bestehend aus ganzen Zahlen
aufsteigend sortiert.
Der Benutzer soll per Eingabe entscheiden,
welche Elemente in die Liste kommen
und er soll so viele Elementen eingeben können,
wie er will. Wenn er mit der Eingabe fertig ist,
soll er mit einem Befehl (zum Beispiel q) die Eingabe beenden.
Hinweis: while
Musterlösung: sortierprogramm.py.
Zusatzaufgabe: Schreibe ein anderes Programm, welches eine Liste aus Zeichenketten alphabetisch sortiert.
10.1.7. Prof. Ungerechtmann
Vorkenntnisse: Kapitel 1 bis 5.
Professor Ungerechtmann der Kantonsschule Unfairdorf braucht ein Programm für die Notenvergabe der Abschlussprüfung. Die Abschlussnote hängt von den folgenden Parametern ab:
Prüfungsnote (von 1 bis 6 mit Halbpunkten);
Augenfarbe (z.B. dunkel=1, hell=0);
Frisur (z.B. kurze Haare=1, lange Haare=0);
Wetter (z.B. schön=1, nicht schön=0).
Es gilt folgendes:
Hat der Prüfling dunkle Augen und…
kurze Haare, so wird die Abschlussnote um 10% erhöht (d.h. Abschlussnote = Prüfungsnote + 10% Prüfungsnote).
lange Haare, so wird die Abschlussnote um 10% reduziert.
Hat der Prüfling helle Augen und…
kurze Haare, so wird die Abschlussnote um 10% reduziert.
lange Haare, so wird die Abschlussnote um 10% erhöht.
Ist das Wetter schön, so wird die Abschlussnote um eine Einheit reduziert.
Die Abschlussnoten müssen auf halbe Noten gerundet werden.
Hinweis: Wie kann man auf halbe Noten runden? Die Funktion round()
rundet auf ganze Noten, z.B. round(5.4) = 5 aber round(5.4*2) = 11… ;)
Musterlösung: ungerechtmann.py.
Zusatzaufgabe: Erfinde und implementiere einige neue Bedingungen, von denen die Abschlussnote abhängt.
10.1.8. Flache Steuern
Vorkenntnisse: Kapitel 1 bis 5.
Der Steueramtchef von Flächenland stellt dich an, um ein einfaches Programm in Python zu schreiben. Dieses Programm soll den Steuersatz jedes Steuerzahlers berechnen. Die Eingabeparameter sind:
Vorname und Nachname des Steuerzahlers
Einkommen (in Dublonen, die Währung von Flächenland)
Die Ausgabe soll von folgender Form sein:
Der Steuerzahler Vorname Nachname muss für das laufende Jahr X Dublonen dem Steueramt bezahlen.
Der Steuersatz wird gemäss folgender Tabelle bestimmt:
Einkommen \(E\) |
Steuersatz |
\(E \le 10'000\) |
40% |
\(10'000 < E \le 30'000\) |
55% |
\(30'000 < E \le 70'000\) |
75% |
\(E > 70'000\) |
82% |
Musterlösung: flache_steuern.py.
Zusatzaufgabe: Berücksichtige in deinem Programm neben dem Einkommen auch das Vermögen.
Vermögen \(H\) |
Steuersatz |
\(H \le 100'000\) |
5% |
\(100'000 < H \le 500'000\) |
8% |
\(500'000 < H \le 1'000'000\) |
13% |
\(H > 1'000'000\) |
21% |
Hat zum Beispiel ein Steuerzahler \(25'000\) Dublonen Einkommen und \(600'000\) Dublonen Vermögen, so muss er
Dublonen dem Steueramt bezahlen.
10.2. Mathematische Probleme
10.2.1. Sum that
Vorkenntnisse: Kapitel 1 bis 5.
Erstelle ein Programm, das die Summe aller natürliche Zahlen \(n \le 10000\) mit \(7 \mid n\) und \(5 \nmid n\) berechnet.
Musterlösung: sum_that.py.
Zusatzaufgabe: List comprehension ist ein syntaktisches Konstrukt, um Listen zu erzeugen. Schau hier wie es in Python funktioniert: https://docs.python.org/3.3/tutorial/datastructures.html#list-comprehensions. Versuche nachher mit diesem Konstrukt ein äquivalentes Programm zu schreiben.
10.2.2. Quadratische Gleichungen
Vorkenntnisse: Kapitel 1 bis 5.
Erstelle ein Programm zur Lösung von quadratische Gleichungen
Die reellen Koeffizienten \(a, b, c\) werden vom Benutzer eingegeben.
Hinweise:
Das Programm kann man elegant gestalten, indem man am Anfang verschiedene Fälle unterscheidet. Was passiert zum Beispiel wenn \(a=0\)? Wenn \(b^2-4ac < 0\)? …
Analog wie die Zahl \(\pi\) kann die Funktion zur Berechnung von Quadratwurzeln (
sqrt) vom Modulemathimportiert werden.
Musterlösung: quadratische_gleichungen.py.
Zusatzaufgabe: Sei eine quadratische Funktion
\(f(x) = ax^2+bx+c\) durch ihre Koeffizienten a, b, c
und eine lineare Funktion \(g(x) = mx + q\) durch m und q gegeben.
Erstelle ein Programm, das die Schnittpunkte
der Graphen von \(f\) und \(g\) berechnet.
10.2.3. Zahlenfolge
Vorkenntnisse: Kapitel 1 bis 5.
Sei \(n \in \mathbb N\). Es gelten folgende Regeln:
Falls \(3 \mid n\), dann soll \(n\) um \(4\) erhöht werden.
Falls \(3 \nmid n\) aber \(4 \mid n\), dann soll \(n\) halbiert werden.
Falls \(3 \nmid n\) und \(4 \nmid n\), dann soll \(n\) um \(1\) verkleinert werden.
Diese Regeln sollen nun sukzessive angewendet werden bis \(n = 0\) ist. Zum Beispiel hat man für \(n = 7\):
In diesem Beispiel braucht man 11 Schritte, um die 0 zu erreichen.
Schreibe ein Programm, welches zu zwei gegebenen natürliche Zahlen
a und b mit a < b,
auf der Konsole die Anzahl benötigte Schritte für jedes \(n\)
(\(a \le n \le b\)) ausgibt.
Für a = 1 und b = 7 soll die Ausgabe folgendermassen aussehen:
1 -> 1
2 -> 2
3 -> 12
4 -> 3
5 -> 4
6 -> 10
7 -> 11
Musterlösung: anzahl_schritte.py.
Zusatzaufgabe: Das Collatz-Problem ist ein ungelöstes mathematisches Problem. Es handelt sich dabei um eine Zahlenfolge, die im Zyklus 4-2-1 mündet, unabhängig davon, welche Startzahl \(n\) gewählt wird. Schaue dir zuerst an, wie die Folge definiert ist und erstelle dann ein Programm, welches bei einer gegeben Startzahl die Anzahl benötigte Schritte für die Erreichung des Zyklus 4-2-1 ausgibt.
10.2.4. PPDI
Vorkenntnisse: Kapitel 1 bis 5.
Die Menge der narzisstischen Zahlen ist eine Teilmenge der natürlicher Zahlen, die durch bestimmte Rechenvorschriften mit ihren Ziffern sich selbst wieder erzeugen (siehe http://de.wikipedia.org/wiki/Narzisstische_Zahl).
Die PPDI (Pluperfect digital invariants, auch Armstrong-Zahlen) sind narzisstische Zahlen, deren Summe ihrer Ziffern, jeweils potenziert mit der Stellenanzahl der Zahl, wieder die Zahl selbst ergibt. Zum Beispiel ist 371 eine PPDI:
Schreibe ein Programm, welches alle PPDIs mit drei Ziffern bestimmt.
Musterlösung: ppdi.py.
10.2.5. 153
Vorkenntnisse: Kapitel 1 bis 6.
Sei \(n>0\) eine ganze Zahl, die durch 3 teilbar ist (zum Beispiel 86145). Die Summe der dritten Potenzen der Ziffern ist wieder eine Zahl, die durch 3 teilbar ist:
Von dieser neuen Zahl kann man nochmals die Summe der dritten Potenzen der Ziffern berechnen und diese ist wieder durch 3 teilbar (\(9^3+1^3+8^3 = 1242\)), usw. Man kann beweisen, dass dieser Vorgang irgendwann zur 153 gelangt und bei dieser Zahl auch bleibt. Man bemerke, dass 153 eine PPDI ist (\(1^3+5^3+3^3 = 153\)).
Erstelle ein Programm, das diese Tatsache verifiziert. Im Programm musst du
eine Funktion quersumme_dritter_potenzen() definieren. Diese Funktion
nimmt als Argument eine ganze Zahl und gibt als Rückgabewert die Summe der
dritten Potenzen der Ziffern dieser Zahl.
Musterlösung: hundertdreiundfuenfzig.py.
10.2.6. Sieb des Eratosthenes
Vorkenntnisse: Kapitel 1 bis 6.
Das Sieb des Eratosthenes ist ein Algorithmus zur Bestimmung einer Liste oder Tabelle aller Primzahlen kleiner oder gleich einer vorgegebenen Zahl.
Aus http://de.wikipedia.org/wiki/Sieb_des_Eratosthenes:
Zunächst werden alle Zahlen 2, 3, 4, … bis zu einem frei wählbaren Maximalwert N aufgeschrieben. Die zunächst unmarkierten Zahlen sind potentielle Primzahlen. Die kleinste unmarkierte Zahl ist immer eine Primzahl. Nachdem eine Primzahl gefunden wurde, werden alle Vielfachen dieser Primzahl als zusammengesetzt markiert. Man bestimmt die nächstgrössere nicht markierte Zahl. Da sie kein Vielfaches von Zahlen kleiner als sie selbst ist (sonst wäre sie markiert worden), kann sie nur durch eins und sich selbst teilbar sein. Folglich muss es sich um eine Primzahl handeln. Diese wird dementsprechend als Primzahl ausgegeben. Man streicht wieder alle Vielfachen und führt das Verfahren fort, bis man am Ende der Liste angekommen ist. Im Verlauf des Verfahren werden alle Primzahlen ausgegeben.
Da ein Primfaktor einer zusammengesetzten Zahl immer kleiner gleich der Wurzel der Zahl sein muss, ist es ausreichend, nur die Vielfachen von Zahlen zu streichen, die kleiner oder gleich der Wurzel der Schranke N sind.

Beispiel mit N = 120. Quelle: http://de.wikipedia.org/wiki/Sieb_des_Eratosthenes
Schreibe ein Programm, das bei einer gegebenen natürliche Zahl \(N \ge 2\), die Liste aller Primzahlen kleiner oder gleich \(N\) erzeugt.
Das Programm soll folgende Struktur haben:
Eine Funktion
sieb()mitNals Eingabeparameter und welche die Liste der Primzahlen kleiner oder gleichNzurückgibt.Eine Funktion
main(), in der der Benutzer zur Eingabe aufgefordert wird und die Funktionsieb()aufruft.Der Aufruf der
main()-Funktion.
Als Test für dein Programm benutze folgende Tatsache: Es gibt 78’498 Primzahlen, welche kleiner als 1’000’000 sind.
Musterlösung: sieb.py.
10.2.7. Zeitmessung
Vorkenntnisse: Kapitel 1 bis 6.
Passe deine Lösung aus der Aufgabe Sieb des Eratosthenes so an,
dass das Programm neben der Liste der Primzahlen,
auch die von der Funktion sieb() benötigte Zeit ausgibt.
Bemerkung
Die Funktion time() aus dem Module time kann dir da
sicher helfen.
Musterlösung: sieb_zeit.py.
10.2.8. Primfaktorzerlegung
Vorkenntnisse: Kapitel 1 bis 6.
Mit Hilfe des Siebs des Eratosthenes sollst du nun ein Programm erstellen, weches die Primfaktorzerlegung einer natürliche Zahl berechnet.
Musterlösung: primfaktorzerlegung.py.
Zusatzaufgabe: Mit Hilfe der bisherigen Programme, welche du geschrieben hast, erstelle nun ein weiteres Programm, welches zu einer gegebenen Zahl \(n\), alle vollkommenen Zahlen kleiner oder gleich \(n\) findet. Was eine vollkommene Zahl ist, kannst du hier nachlesen: http://de.wikipedia.org/wiki/Vollkommene_Zahl.
10.2.9. Monty Hall Problem
Vorkenntnisse: Kapitel 1 bis 8.
Das Monty-Hall-Problem (auch Ziegenproblem) ist eine Aufgabe mit Bezug zur Wahrscheinlichkeitstheorie. Aus http://de.wikipedia.org/wiki/Ziegenproblem:
Nehmen Sie an, Sie wären in einer Spielshow und hätten die Wahl zwischen drei Toren. Hinter einem der Türen ist ein Auto, hinter den anderen sind Ziegen. Sie wählen eine Tür, sagen wir, Tür A, und der Showmaster, der weiss, was hinter den Türen ist, öffnet eine andere Tür, sagen wir, Tür C, hinter dem eine Ziege steht. Er fragt Sie nun: "Möchten Sie die Tür B?" Ist es von Vorteil, die Wahl der Tür zu ändern?
Selbst wenn du die Frage jetzt noch nicht beantworten kannst,
versuche dieses Spiel mit einer graphischen Benutzeroberfläche
zu implementieren. Benutze dazu das Modul tkinter.
Bemerkung
Es gibt keine richtige oder falsche Art, ein solches Programm zu schreiben. Hier gibt es aber einige Hinweise, die für die Erstellung nützlich sein können. Du musst sie aber nicht unbedingt befolgen!
Hinweise:
indicate_goat(n): eine Funktion, die bei gegebener Tür (n=0,1oder2) eine andere Tür anzeigt, hinter welcher sich eine Ziege befindet.Aufgepasst: Falls der Spieler am Anfang „eine Ziege“ wählt, gibt es nur eine einzige Möglichkeit. Falls er aber „das Auto“ wählt, kann der Showmaster eine der beiden anderen Türen öffnen. Damit das Spiel fair bleibt, soll er zufällig eine Türe wählen.
Die drei Türen können als Buttons implementiert werden. In diesem Fall kann man drei Funktionen definieren (z.B.
def doorA_action(), …). das Programm soll aber irgendwie die zwei Situationen (erste oder zweite Wahl) erkennen.Hilfreiche Funktion:
configure()(siehe https://docs.python.org/3.3/library/tkinter.html#setting-options). Zum BeispieldoorA.configure(state=DISABLED)deaktiviert ButtondoorA.
Musterlösung: monty_hall.py. Diese Musterlösung enthält 3
Bilder. Um diese Datei korrekt auszuführen muss man auch diese Bilder
herunterladen:
door.gif,
fiat500.gif,
Boer-Goat.gif.
Zusatzaufgabe: Ergänze dein Programm z.B. mit einer Menüleiste, Informationen über die Version oder die Entwickler, …
10.3. Objektorientierte Aufgaben
10.3.1. Fahrrad
Vorkenntnisse: Kapitel 1 bis 7.
Erstelle eine Klasse Fahrrad. Die Instanzen dieser Klasse sollen folgende
Attribute besitzen:
eine Zeichenkette
__marke(private): das Attribut beschreibt die Marke des Fahrradseine positive ganze Zahl
__anz_zahnkraenze(private): diese Attribut beschreibt die Anzahl Zahnkränze des Fahrrads.eine positive ganze Zahl
__anz_ritzel(private): diese Attribut beschreibt die Anzahl Ritzel des Fahrrads.eine positive ganze Zahl
_zahnkranz(protected): diese Attribut beschreibt den gegenwärtige Zahnkranz des Fahrrads.eine positive ganze Zahl
_ritzel(protected): diese Attribut beschreibt das gegenwärtige Ritzel des Fahrrads.
Ausserdem soll die Klasse folgenden Methoden besitzen:
get_marke(): gibt die Marke zurück.get_anz_zahnkraenze(): gibt die Anzahl Zahnkränze zurück.get_anz_ritzel(): gibt die Anzahl Ritzel zurück.get_zahnkranz(): gibt den gegenwärtigen Zahnkranz zurück.get_ritzel(): gibt das gegenwärtige Ritzel zurück.up_zahnkranz(): verschiebt die Kette über den nächsten Zahnkranz (wenn möglich).down_zahnkranz(): verschiebt die Kette über den vorherigen Zahnkranz (wenn möglich).up_ritzel(): verschiebt die Kette über das nächste Ritzel (wenn möglich).down_ritzel(): verschiebt die Kette über das vorherigen Ritzel (wenn möglich).print_zustand(): gibt den gegenwärtigen Zustand des Fahrrads in folgender Form:MyBike *o----ooo*ooooo
wobei in diesem Fall
marke=MyBike;*obedeutet, dass das Fahrrad zwei Zahnkränze hat und der gegenwärtige, der erste ist;----ist die Kette;ooo*ooooobedeutet, dass das Fahrrad neun Ritzel hat und das gegenwärtige, das vierte ist.
__marke, __anz_zahnkraenze und __anz_ritzel sind private und
dürfen nicht von Aussen geändert werden. Sie können allerdings durch den
getter-Methoden gelesen werden.
_zahnkranz und _ritzel sind protected und sollten eigentlich nicht
direkt geändert werden, sondern nur mit den entsprechenden
up-down-Methoden.
Als Grundlage kannst du folgendes Muster benutzen:
1class Fahrrad: 2 3 ''' 4 Hier definierst du die Methoden (__init__() Methode nicht vergessen) 5 ''' 6 7 8def main(): 9 f = Fahrrad("Mountain Bike", 3, 10, 2, 5) 10 f.print_zustand() 11 f.up_ritzel() 12 f.print_zustand() 13 f.up_zahnkranz() 14 f.up_zahnkranz() 15 f.print_zustand() 16 f.down_zahnkranz() 17 f.up_ritzel() 18 f.up_ritzel() 19 f.up_ritzel() 20 f.up_ritzel() 21 f.print_zustand() 22 f.down_zahnkranz() 23 f.down_ritzel() 24 f.down_ritzel() 25 f.down_ritzel() 26 f.print_zustand() 27 f.down_zahnkranz() 28 f.print_zustand() 29 f.down_zahnkranz() 30 f.print_zustand() 31 g = Fahrrad("Mein Velo", 2, 5, 1, 1) 32 g.print_zustand() 33 print(g.get_marke(), "hat", g.get_anz_ritzel(), "Ritzel und", g.get_anz_zahnkraenze(), "Zahnkränze") 34 35main()
Falls aller korrekt implementiert wird, soll die Ausgabe Folgende sein:
Mountain Bike o*o----oooo*ooooo
Mountain Bike o*o----ooooo*oooo
Mountain Bike oo*----ooooo*oooo
Mountain Bike o*o----ooooooooo*
Mountain Bike *oo----oooooo*ooo
Mountain Bike *oo----oooooo*ooo
Mountain Bike *oo----oooooo*ooo
Mein Velo *o----*oooo
Mein Velo hat 5 Ritzel und 2 Zahnkränze
Der Inhalt der main()-Methode kannst du allerdings ändern.
Musterlösung: fahrrad_aufgabe.py.
Zusatzaufgabe: Erstelle eine Klasse Radfahrer(). Erfinde und implementiere neue Instanzvariablen und Methoden für beide Klassen. Beispiel: ein Fahrrad gehört zu einem Radfahrer und umgekehrt ein Radfahrer besitzt eine Liste von Fahrräder; ein Radfahrer kann ein von seinen Fahrräder einem anderen Radfahrer schenken; …
10.3.2. Sparse vectors
Vorkenntnisse: Kapitel 1 bis 7.
In der Mathematik und in der Informatik bezeichnet man als schwachbesetzte oder dünnbesetzte Matrix (auf English: sparse matrix) eine Matrix, bei der so viele Einträge aus Nullen bestehen, dass es sich lohnt, dies auszunutzen. Analog wird ein Vektor, der zu einem Grossteil aus Nullen besteht, als schwachbesetzter Vektor (auf English: sparse vector) bezeichnet. Beispiel:
All die Nullen zu spreichern, wäre eine Spreicherverschwendung. Man könnte zum Beispiel vorheriges Vektor, wie folgt darstellen:
Dies liesst sich wie folgt: An der 1. Stelle ist eine 1, an der 6. Stelle eine 3 und an der 13. Stelle eine 1.
Bemerkung
Pass auf die Indizes auf! In der Mathematik beginnen die Indizes eines Vektors normalerweise bei der 1; in der Informatik bei der 0.
Schreibe eine Klasse Sparse(), die schwachbesetzte Vektoren darstellt.
Diese Klasse soll nützliche Funktionen anbieten, die zum Beispiel erlauben, den
Betrag eines Vektors zu berechnen, den Gegenvektor zu bestimmen, einen Eintrag
zu verändern oder den Vektor auf der Konsole ausgibt
(in kompakter oder vollständiger Schreibweise).
Implementiere ebenfalls die folgenden Funktionen:
eine Funktion
add_sparse(a, b), welche aus den zwei Sparse Vektorenaundbdie Summe bildet und diesen als neuesSparse-Objekt zurückgibt.eine Funktion
dot_sparse(a, b), welche das Skalarprodukt der beiden Sparse Vektoren berechnet und zurückgibt.eine Funktion
create_random_sparse(n,m,a,b), die ein Objekt der KlasseSparsemit den folgenden Eigenschaften erzeugt:Dimension
nhöchstens
mvon Null verschiedene Einträge, deren Wert im Intervall[a,b]liegen. Diese Einträge sind zufällig im ganzen Vektor verteilt.
Hinweise:
Achtung!
>>> vector1 = [1, 3, 7, 9, 0] >>> vector2 = vector1 >>> vector2[0] = 5 >>> vector1 [5, 3, 7, 9, 0]
Bei der Zuordnung``vector2 = vector1`` wird keine Kopie der Liste erzeugt, sondern eine Referenz auf das gleiche Objekt (siehe auch Kapitel Listen).
Um denoch eine Kopie zu erstellen, benutze folgenden Befehl:
>>> vector3 = vector2[:] >>> vector3[0] = 400 >>> vector2 [5, 3, 7, 9, 0] >>> vector3 [400, 3, 7, 9, 0]
Der Ausdruck
vector2[:]gibt nur die Werten der Liste zurück.
Musterlösung: sparse.py.
Zusatzaufgabe: Implementiere eine zusätzliche Funktion, die den Winkel zwischen zwei gegeben Sparse Vektoren bestimmt.
10.4. Kryptographie
10.4.1. Caesar-Verschlüsselung
Vorkenntnisse: Kapitel 1 bis 6.
Die Caesar-Verschlüsselung ist ein einfaches Verschlüsselungsverfahren. Aus http://de.wikipedia.org/wiki/Caesar-Verschl%C3%BCsselung:
Bei der Verschlüsselung wird jeder Buchstabe des Klartexts auf einen Geheimtextbuchstaben abgebildet. Diese Abbildung ergibt sich, indem man die Zeichen eines geordneten Alphabets um eine bestimmte Anzahl zyklisch nach rechts verschiebt (rotiert). Die Anzahl der verschobenen Zeichen bildet den Schlüssel, der für die gesamte Verschlüsselung unverändert bleibt.
Zum Beispiel wird der Klartext Python mit dem Schlüssel 2 in den Geheimtext
Sbwkrq abgebildet.
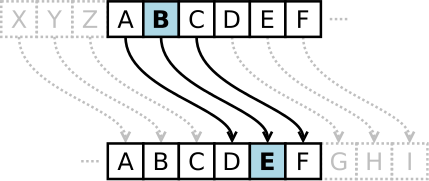
Schematische Darstellung einer Verschiebechiffre mit Verschiebung um drei Buchstaben.
Implementiere eine Caesar-Verschlüsselung.
Beachte folgendes:
>>> ord('A')
65
>>> ord('Z')
90
>>> ord('a')
97
>>> ord('z')
122
>>> chr(ord('a')+1)
'b'
Musterlösung: caesar.py.
Zusatzaufgabe: Passe dein Programm so an, dass es ganze .txt-Files
verschlüsseln kann. Die Seite
https://docs.python.org/3.3/tutorial/inputoutput.html#reading-and-writing-files
kann dir dabei sicher helfen.
10.4.2. Häufigkeitsanalyse
Vorkenntnisse: Kapitel 1 bis 6.
Die Häufigkeitsanalyse ist eine Methode der Kryptoanalyse. Aus http://de.wikipedia.org/wiki/H%C3%A4ufigkeitsanalyse:
Die Häufigkeitsanalyse dient der Entschlüsselung von Geheimtexten ohne bekannten Klartext. Die einzelnen Buchstaben werden dabei gezählt und ihre Häufigkeit notiert, meist in Prozent, also relativ zur Gesamtzahl der Buchstaben (Buchstabenhäufigkeit).
Nun kann aufgrund der spezifischen Häufigkeit spezieller Buchstaben in einer Sprache, das E beispielsweise kommt in der deutschen Sprache mit rund 17 % mit Abstand am häufigsten vor, auf das verwendete Alphabet geschlossen werden. Kommt in einer Nachricht also beispielsweise der ansonsten recht seltene Buchstabe Q mit etwa 17 % vor, so liegt der Schluss nahe, dass Q in dieser Verschlüsselung für das E steht. Falls mehrere Möglichkeiten der Zuordnung bestehen, kann man die gleiche Vorgehensweise zusätzlich auch auf Bigramme, also Buchstabenpaarungen, anwenden. Da die Genauigkeit der Häufigkeit mit der Länge einer Nachricht steigt, ist eine lange Nachricht deutlich einfacher zu entschlüsseln, als eine kurze.
Schreibe ein Programm, welches zu einer gegebenen .txt-Datei,
die Häufigkeitsanalyse der Buchstaben in der Datei durchführt.
Hinweis: Eine Unterscheidung zwischen Gross- und Kleinbuchstaben ist nicht notwendig. Ignoriere ausserdem alle Sonderzeichen/-laute (ü, à, $, …).
Von http://www.gutenberg.org/ kann man gratis einige Bücher im .txt-Format
herunterladen. Teste dein Programm mit einem solchen Buch (zum Beispiel
Adventure of Huckleberry Finn:
http://www.gutenberg.org/cache/epub/76/pg76.txt)
Musterlösung: frequency_analysis.py,
pg76.txt.
Zusatzaufgabe: Implementiere eine graphische Oberfläche, welche die
Häufigkeitsanalyse als Histogramm darstellt.
Die Bibliothek matplotlib kann dir vielleicht helfen ein Histogramm
darzustellen. Sie befindet sich jedoch nicht in den Standardlibraries von
Python und muss eventuell nachinstalliert werden.